2nd Chapter - Polynomials

Exercise 2.1

Question 1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Answer
(i)the graph does not intersect the x axis so that there are no zero in this graph
(ii)the graph intersects the x axis at one places so that here are one zeros in this graph
(iii)the graph intersects the x axis at three places so that there are three zeros in this graph
(iv)the graph intersects the x axis at two places so there are two zeros in this graph
(v) the graph intersect the x axis at four places so there are four zeros in this graph
(vi) the graph intersects the x axis at three places so that there are three zeros in this graph

Exercise 2.2

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Solution:


Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:

Solution:

Exercise 2.3

Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2
Solution:

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:

Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are and and –
Solution:

Question 4.
On dividing x3 – 3x2 + x + 2bya polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:

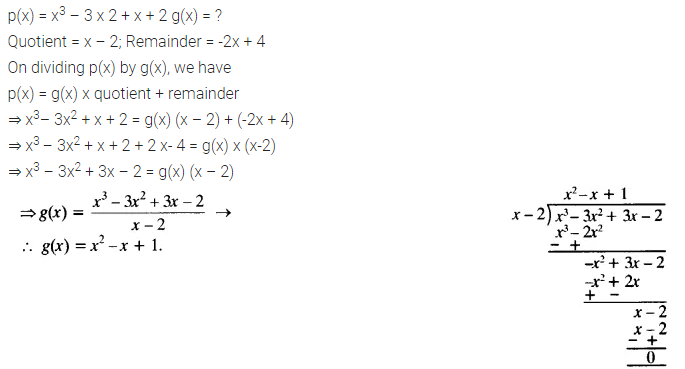
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:

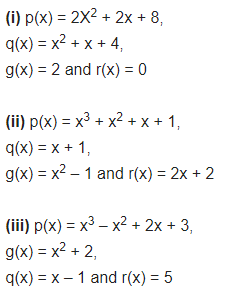
Exercise 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; , 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:

Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:

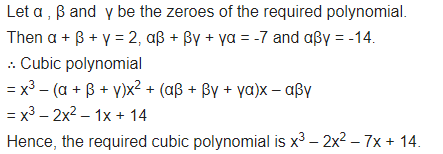
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:

Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution: